图

辅助函数

1. FirstNeighbor(G,x)：

   • 求图G中顶点x的第一个邻接点，若有则返回顶点号。

   • 若x没有邻接点或图中不存在x，则返回-1。

2. NextNeighbor(G,x,y)：

   • 假设图G中顶点y是顶点x的一个邻接点，返回除y之外，顶点x的下一个邻接点的顶点号
   • 若y是x的最后一个邻接点，则返回-1。

邻接矩阵表示法

假设图 G 使用邻接矩阵表示，G.matrix[i][j] 为 1 表示顶点 i 和顶点 j 之间有边，为 0 表示没有边。

#define MAX_VERTEX_NUM 100

typedef struct {
    int numVertices;
    int matrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
} Graph;

// 返回顶点v的第一个邻接顶点
int FirstNeighbor(Graph G, int v) {
    for (int i = 0; i < G.numVertices; ++i) {
        if (G.matrix[v][i] == 1) {
            return i;
        }
    }
    return -1; // 没有邻接顶点
}

// 返回顶点v的邻接顶点w之后的下一个邻接顶点
int NextNeighbor(Graph G, int v, int w) {
    for (int i = w + 1; i < G.numVertices; ++i) {
        if (G.matrix[v][i] == 1) {
            return i;
        }
    }
    return -1; // 没有更多的邻接顶点
}

邻接表表示法

如果图 G 使用邻接表表示，G.adjList 是一个包含每个顶点的邻接顶点列表的数组。

#include <vector>

#define MAX_VERTEX_NUM 100

typedef struct {
    int numVertices;
    std::vector<int> adjList[MAX_VERTEX_NUM];
} Graph;

// 返回顶点v的第一个邻接顶点
int FirstNeighbor(Graph G, int v) {
    if (!G.adjList[v].empty()) {
        return G.adjList[v][0];
    }
    return -1; // 没有邻接顶点
}

// 返回顶点v的邻接顶点w之后的下一个邻接顶点
int NextNeighbor(Graph G, int v, int w) {
    for (size_t i = 0; i < G.adjList[v].size(); ++i) {
        if (G.adjList[v][i] == w) {
            if (i + 1 < G.adjList[v].size()) {
                return G.adjList[v][i + 1];
            }
            break;
        }
    }
    return -1; // 没有更多的邻接顶点
}

FirstNeighbor(Graph G, int v):

• 邻接矩阵版本：遍历顶点 v 的所有可能邻接顶点（从 0 到 G.numVertices - 1），如果找到一个顶点 i 与顶点 v 有边（G.matrix[v][i] == 1），则返回这个顶点 i。如果没有找到，则返回 -1。
• 邻接表版本：直接返回顶点 v 的邻接顶点列表的第一个元素。如果列表为空，则返回 -1。

NextNeighbor(Graph G, int v, int w):

• 邻接矩阵版本：从顶点 w + 1 开始，遍历顶点 v 的所有可能邻接顶点，找到第一个与顶点 v 有边的顶点 i（G.matrix[v][i] == 1），返回这个顶点 i。如果没有找到，则返回 -1。
• 邻接表版本：在顶点 v 的邻接顶点列表中，找到顶点 w，然后返回其后的下一个顶点。如果 w 是最后一个邻接顶点或没有更多邻接顶点，则返回 -1。

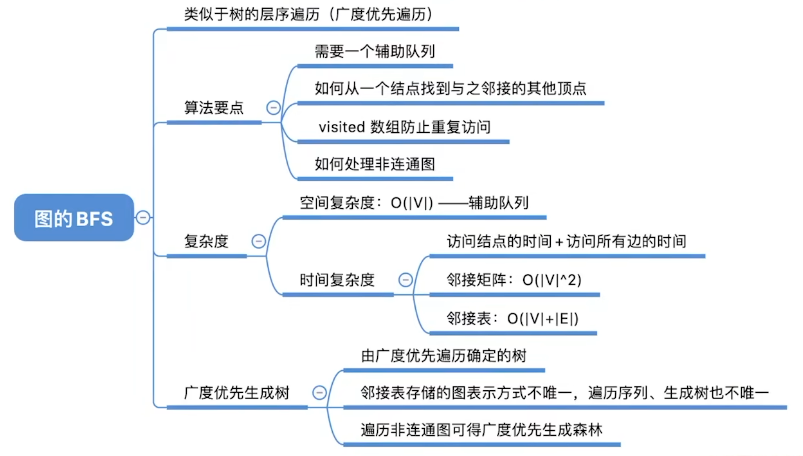
广度优先遍历

广度优先遍历（Breadth-First-Search, BFS）要点：

1. 找到与一个顶点相邻的所有顶点
2. 标记哪些顶点被访问过
3. 需要一个辅助队列

BFS

bool visited[MAX_VERTEX_NUM]; // 访问标记数组

// 广度优先遍历
void BFS(Graph G, int v) { // 从顶点v出发，广度优先遍历图G
    visit(v); // 访问初始顶点v
    visited[v] = TRUE; // 对v做已访问标记
    Enqueue(Q, v); // 顶点v入队列Q

    while (!isEmpty(Q)) {
        DeQueue(Q, v); // 出队列顶点v

        for (int w = FirstNeighbor(G, v); w >= 0; w = NextNeighbor(G, v, w)) { // 检测v所有邻接点
            if (!visited[w]) { // w为v的尚未访问的邻接顶点
                visit(w); // 访问顶点w
                visited[w] = TRUE; // 对w做已访问标记
                EnQueue(Q, w); // 顶点w入列
            }
        }
    }
}

执行顺序解析：

1. **初始化邻接顶点 w**：int w = FirstNeighbor(G, v);，返回顶点 v 的第一个邻接顶点 w。

2. 检查是否有邻接顶点：w >= 0

   • 如果 w 为负数（例如，-1），表示没有邻接顶点，跳出循环。
   • 如果 w 为非负数，表示有邻接顶点，进入循环体。

3. 检查顶点 w 是否已访问：if (!visited[w])

   • 检查 visited[w] 是否为 false，即顶点 w 是否尚未被访问。

4. 访问尚未访问的邻接顶点 w:

   • 如果未被访问，执行以下步骤：

     visited[w] = TRUE; // 对w做已访问标记
     EnQueue(Q, w); // 顶点w入队

     • 调用 visit(w) 函数，对顶点 w 进行访问（例如，打印顶点或进行其他处理）。
     • 将 visited[w] 设为 TRUE，标记顶点 w 已被访问。
     • 将顶点 w 入队列 Q，以便在之后的 BFS 阶段继续处理。

5. 更新邻接顶点 w 为下一个邻接顶点：w = NextNeighbor(G, v, w);

   • 调用 NextNeighbor(G, v, w) 函数，返回顶点 v 的下一个邻接顶点，更新 w 的值。

6. 重复步骤 2 到 5:

   • 继续循环，检查新的 w 是否非负，并按照上述步骤处理新的邻接顶点。

遍历序列的可变性

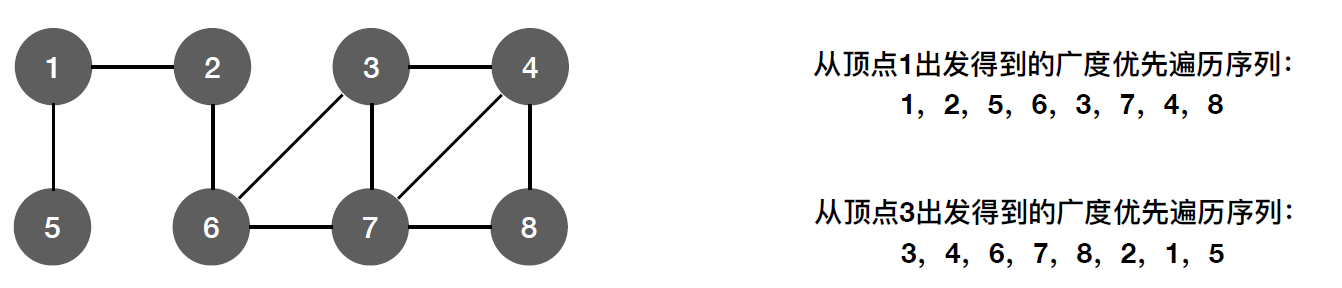
同一个图的邻接矩阵表示方式唯一，因此广度优先遍历序列唯一
同一个图邻接表表示方式不唯一，因此广度优先遍历序列不唯一

上述算法存在的问题

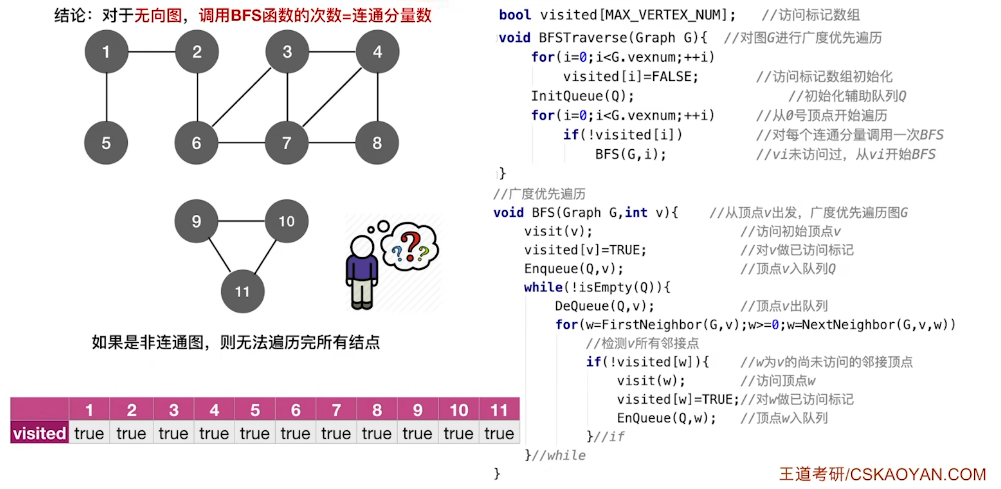
如果是非连通图，则无法遍历完所有结点。

要解决不能遍历非连通图的问题，可以在调用 BFS 之前或之后添加一个遍历所有顶点的循环，对于尚未访问的顶点，启动一次新的 BFS。这确保了图中所有连通分量都被遍历。

对于无向图，调用BFS函数的次数=连通分量数

// 遍历整个图，处理非连通图的情况
void BFSTraverse(Graph G) {
    for (int i = 0; i < G.Vexnum; ++i) {
        visited[i] = false; // 初始化访问标记数组
    }
    InitQueue(Q);	///初始化辅助队列Q
    for (int i = 0; i < G.Vexnum; ++i) {
        if (!visited[i]) {
            BFS(G, i); // 对尚未访问的顶点调用BFS
        }
    }
}

复杂度分析

1. 空间复杂度：最坏情况，辅助队列大小为 O(|V|)
2. 时间复杂度
   • 邻接矩阵存储的图：访问 V 个顶点需要O(|V|)的时间。查找每个顶点的邻接点都需要O(|V|)的时间，而总共有|V|个顶点，时间复杂度= O(|V|^2^)
     • 总的时间复杂度为 O(|V|^2^)，忽略低阶
   • 邻接表存储的图：访问 V 个顶点需要O(|V|)的时间，查找各个顶点的邻接点共需要O(2E)的时间（E为所有边数）
     • 总的时间复杂度为：时间复杂度= O(|V|+|E|)

广度优先生成树：

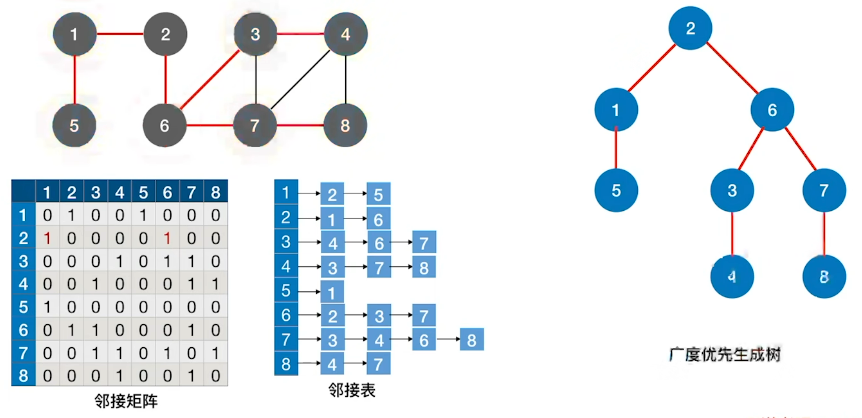
• 广度优先生成树由广度优先遍历过程确定。
• 由于邻接表的表示方式不唯一，因此基于邻接表的广度优先生成树也不唯一
• 对非连通图的广度优先遍历，可得到广度优先生成森林

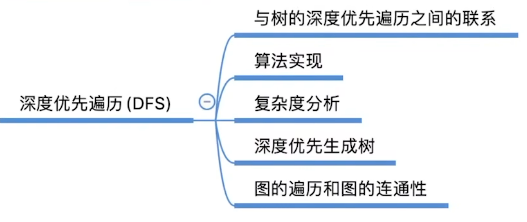
深度优先遍历

bool visited[MAX_VERTEX_NUM]; // 访问标记数组

void DFS(Graph G, int v) {
    visit(v); // 访问顶点v
    visited[v] = true; // 设已访问标记

    // 从顶点v出发，深度优先遍历图G
    for (int w = FirstNeighbor(G, v); w >= 0; w = NextNeighbor(G, v, w)) {
        // 检测v的所有邻接点
        if (!visited[w]) {
            DFS(G, w); // 递归调用DFS
        }
    }
}

和之前一样，会出现无法遍历非连通图的问题

需要加上

void DFSTraverse(Graph G) {
    // 初始化访问标记数组
    for (int v = 0; v < G.vexnum; ++v) {
        visited[v] = false;
    }

    // 对图中的每个顶点执行 DFS
    for (int v = 0; v < G.vexnum; ++v) {
        if (!visited[v]) {
            DFS(G, v);
        }
    }
}

复杂度和BFS一样。

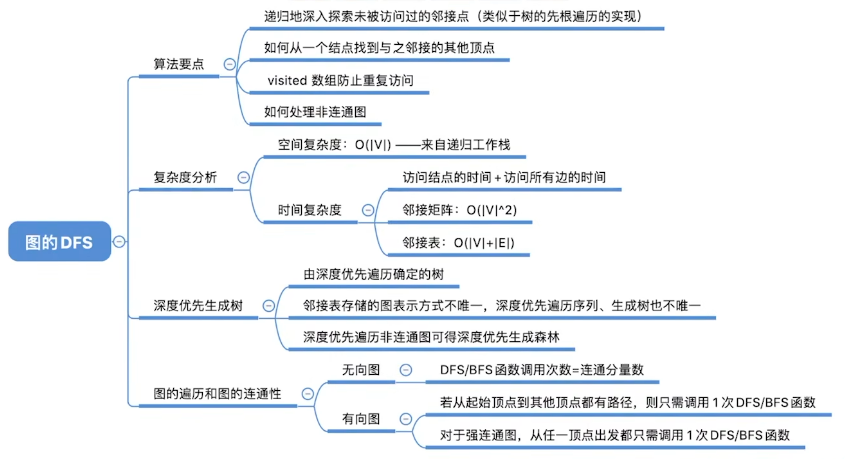
• 同一个图的邻接矩阵表示方式唯一，因此深度优先遍历序列唯一，深度优先生成树也唯一
• 同一个图邻接表表示方式不唯一，因此深度优先遍历序列不唯一，深度优先生成树也不唯一

最小生成树

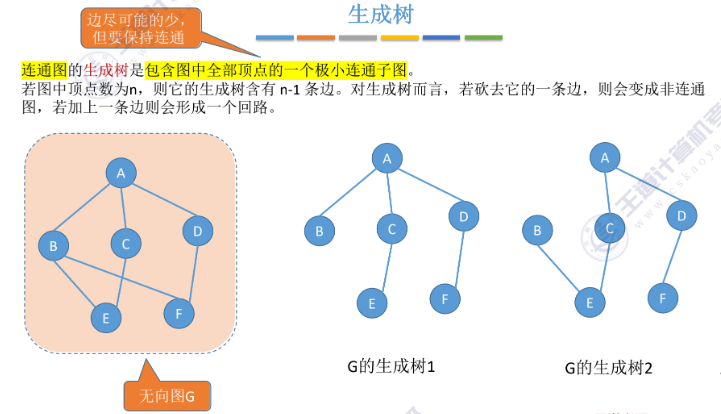
生成树：

连通图的生成树是包含图中全部顶点的一个极小连通子图。

若图中顶点数为n，则它的生成树含有n-1条边。对生成树而言，若砍去它的一条边，则会变成非连通图，若加上一条边则会形成一个回路

最小生成树（最小代价树）：

对于一个带权连通无向图G = (V, E)，生成树不同，每棵树的权（即树中所有边上的权值之和）也可能不同

设R为G的所有生成树的集合，若T为R中边的权值之和最小的生成树，则T称为G的最小生成树（Minimum-Spanning-Tree, MST）

最小生成树可能有多个，但边的权值之和总是唯一且最小的

最小生成树的边数 = 顶点数 - 1

砍掉一条则不连通，增加一条边则会出现回路

如果一个连通图本身就是一棵树，则其最小生成树就是它本身

只有连通图才有生成树，非连通图只有生成森林

求最小生成树的两种方法

Prim算法

Kruskal算法

Prim算法(普里姆)：从某一个顶点开始构建生成树;每次将代价最小的新顶点纳入生成树，直到所有顶点都纳入为止。时间复杂度: O(V2)适合用于边稠密图。

Kruskal算法(克鲁斯卡尔)：每次选择一条权值最小的边，使这条边的两头连通(原本已经连通的就不选)直到所有结点都连通。时间复杂度: O(lEllog2lEl )适合用于边稀疏图。

Prim 算法（普里姆）：

算法思想：

从某一个顶点开始构建生成树；

每次将代价最小的新顶点纳入生成树，直到所有顶点都纳入为止。

时间复杂度：O(|V|^2)，适合用于边稠密图