查找

线性结构

顺序查找

又称为线性查找，它对顺序表和链表都是适用的。

基本思想：其实就是挨个找（从头到jio or 反着来都可以）。

代码实现：

typedef struct{				//查找表的数据结构（顺序表）
    ElemType *elem;			//动态数组基址
    int TableLen;			//表的长度
}SSTable;

//顺序查找
int Search_Seq(SSTable ST,ElemType key){
    int i;
    for(i=0;i<ST.TableLen && ST.elem[i]!=key;++i);
    // 查找成功返回数组下标，否则返回-1
    	return i=ST.TableLen? -1 : i;
}

哨兵版

typedef struct{				//查找表的数据结构（顺序表）
    ElemType *elem;			//动态数组基址
    int TableLen;			//表的长度
}SSTable;

//顺序查找
int Search_Seq(SSTable ST,ElemType key){
    ST.elem[0]=key;
    int i;
    for(i=ST.TableLen;ST.elem[i]!=key;--i)
    // 查找成功返回数组下标，否则返回0
	    return i;
}

注：

一个成功结点的查找长度 = 自身所在层数
一个失败结点的查找长度 = 其父节点所在
层数默认情况下，各种失败情况或成功情况都等概率发生

折半查找

又称二分查找，它仅适用于有序的顺序表。

基础思想：

在[low,high]之间寻找目标关键字，每次检查mid=(low,high)/2（向上或者向下取整）。
根据mid所指元素与目标关键字的大小调整[low,high]的区间。
若low>high则查找失败。
代码实现：

typedef struct{
    ElemType *elem;
    int TableLen;
}SSTable;

// 折半查找
int Binary_Search(SSTable L,ElemType key){
    int low=0,high=L.TableLen,mid;
    while(low<=high){
        mid=(low+high)/2;
        if(L.elem[mid]==key)
            return mid;
        else if(L.elem[mid]>key)
            high=mid-1;					//从前半部分继续查找
        else
            low=mid+1;					//从后半部分继续查找
    }
    return -1;
}

折半查找判定树的构造（爱考）：取决于mid的取值是向上取整还是向下取整。

若mid=⌊ (low+high)/2⌋，则对于任何⼀个结点，必有：右⼦树结点数 - 左⼦树结点数 = 0 或 1。
反之向上取整就是：左⼦树结点数 - 右⼦树结点数 = 0 或 1。
折半查找的判定树⼀定是平衡⼆叉树。折半查找的判定树中，只有最下⾯⼀层是不满的。因此，元素个数为 n 时树⾼ h=⌈log2(n+1)⌉ 。
判定树结点关键字：左<中<右，满⾜⼆叉排序树的定义。失败结点：n+1个（等于成功结点的空链域数量）
时间复杂度：O(log2n)

分块查找

又称为“索引顺序查找”，块内⽆序、块间有序。

基础思想:

索引表记录每个分块的最大关键字、分块的区间
先查索引表(顺序或折半)、再对分块内进行顺序查找
查找效率分析（ASL）:ASL = 查索引表的平均查找长度+查分块的平均查找长度

(设n个记录均匀分为b块,每块s个记录)

顺序查找索引表

树型结构

mindmap
  root((二叉排序树))
    定义
      子节点<值小于父节点
      子节点>值大于父节点
      子树也是BST
    查找操作
      根节点开始
      值等于当前节点->查找成功
      值小于当前节点->递归左子树
      值大于当前节点->递归右子树
      空节点->查找失败
    插入操作
      根节点开始
      值小于当前节点->递归左子树
      值大于当前节点->递归右子树
      空位置->插入新节点
    删除操作
      找到节点
      无子节点->直接删除
      一个子节点->用子节点替代
      两个子节点->用右子树最小节点或左子树最大节点替代
    查找效率分析
      最好情况->O(log n)
      最坏情况->O(n)

二叉排序树(BST)

结构图

构造一颗二叉排序树的目的并不是排序，而是提高查找、插入和删除关键字的速度，这种非线性结构也有利于插入和删除的实现。

定义：二叉排序树又称为二叉查找树（BST,Binary Search Tree)，

一棵二叉树或者是空二叉树，或者是具有如下性质的二叉树：

左子树节点值 < 根节点值 < 右子树节点值
左子树和右子树又各是一棵二叉排序树
进行中序遍历，可得到一个递增序列

查找

若树非空，目标值与根结点的值比较
若相等，则查找成功
若小于根结点，则在左子树上查找，否则在右子树上查找
查找成功，返回结点指针；查找失败返回NULL

typedef struct BSTNode{
    int key;
    struct BSTNode *lchild, *rchild;
}BSTNode, *BSTree;

//查找（非递归）
BSTNode *BST_Search(BiTree T, ElemType key)
{
    while(T != NULL && key != T->data)    //若树空或等于根结点数，则结束循环
    {
        if(key < T->data)    //小于，则在左子树上查找
            T = T->lchild;
        eles    			//大于，则在右子树查找
            T = T->rchild;
    }
    return T;    //失败会返回NULL
}

//查找（递归）
BSTNode *BST_Search(BiTree T, ElemType key)
{
    if(T == NULL)
        return NULL;
    if(key == T->key)
        return T;
    else if(key < T->key)
        return BST_Search(T->lchild, key);
    else
        return BST_Search(T->rchild, key);
}

BST是一种动态生成的树表，通过查找比较不断生成。

插入

若原二叉排序树为空，则直接插入结点；

否则，若关键字k小于根结点值，则插入到左子树，

若关键字k大于根结点值，则插入到右子树

在子树中继续重复以上操作，直到节点插入到对应的叶节点位置上

递归实现

//最坏空间复杂度O(h)
int BST_Insert(BiTree &T, DataType k)
{
    if(T == NULL)
    {
        T = (BiTree)malloc(sizeof(BSTNode));
        T->data = k;
        T->lchild = T->rchild = NULL;
        return 1;
    }
    else if(k == T->data)
        return 0;
    eles if(k < T->data)
        return BST_Insert(T->lchild, k);
    else
        return BST_Insert(T->rchild, k);
}

非递归实现

```





#### 构造

从空树开始依次输入元素，调用插入函数，逐渐构造出一棵树。

```c
void Creat_BST(BiTree &T, DataType str[], int n)
{
    T = NULL;
    int i = 0;
    while(i<n)
    {
        BST_Insert(T, str[i++]);
    }
}

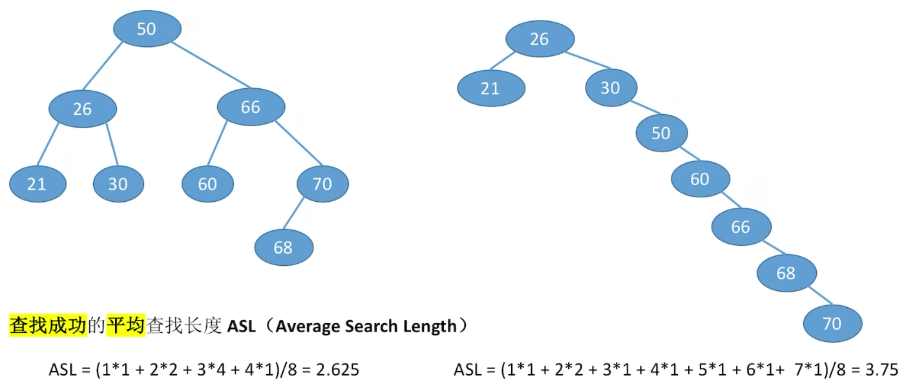
按照序列 str=｛50,66,60,26,21,30,70,68}建立BST
按照序列 str=｛50,26,21,30,66,60,70,68}建立BST
按照序列 str=｛26,21,30,50,60,66,68,70}建立BST

注：不同的关键字序列可能得到相同的二叉排序树，也可能得到不同的二叉排序树

删除

需要保证删除该节点后，仍保持BST特征。

若删除的是叶节点，则直接删除，不会破坏BST性质
若要删除节点Z只有一棵左子树或右子树，则直接让Z的孩子替代它的位置
若删除节点z有左右两棵子树，则令z的值直接被修改为其直接后继（或直接前驱）的值，然后从二叉排序树中删除这个直接后继（或前驱），这样就转换成情况1、2
- 使用直接后继的值覆盖：z的后继是右子树中最左下结点（该节点一定没有左子树)
- 使用直接前驱的值覆盖：z的前驱是左子树中最右下结点（该节点一定没有右子树)

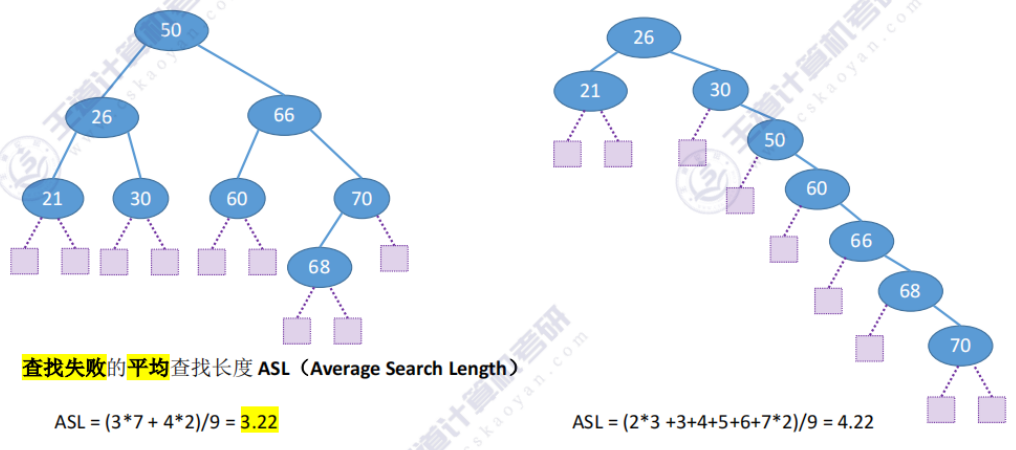
效率分析：（与树高相关）

查找长度：在查找运算中，需要对比关键字的次数称为查找长度，反映了查找操作时间复杂度

BST中某个元素的比较次数 = 该节点所在层的层数。

最好情况：n个结点的二叉树最小高度为[log2n]+1，平均查找长度=O(log2n)
最坏情况：每个结点只有一个分支，树高h=结点数n，平均查找长度=O(n)

查找成功

查找失败

平衡二叉树（AVL）

为了让二叉树在构建的过程中尽可能的保持平衡，即让树的高度最小，引入了平衡二叉树。

平衡二叉树：在插入和删除节点时保证任意结点的左右子树高度差的绝对值小于1，简称AVL（由其发明人的名字取得）

平衡因子：左子树的高 - 右子树的高（只能是 -1，0，1）

//平衡二叉树结点
typedef struct AVLNode{
    int key; 		//数据域
    int balance; 	////平衡因子
    struct AVLNode *lchild, *rchild;
}AVLNode, *AVLTree;

研究的重点就是插入的时候怎么保持树的平衡

插入

从插入点往上找到第一个不平衡结点，调整以该结点为根的子树（最小不平衡子树），只要将最小不平衡子树调整平衡，则其他结点都会恢复平衡

根据不平衡出现的原因，分为4种情况：

LL型：相当于把B的右边部分拽下来保持平衡

右单旋

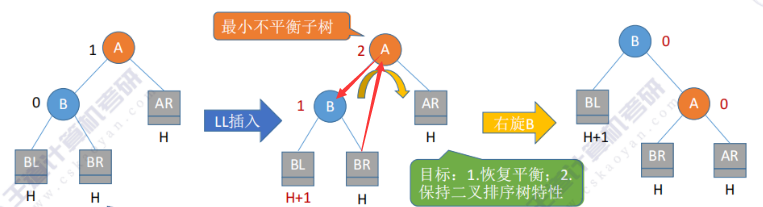
RR型：相当于把B的左边部分拽下来保持平衡

左单旋

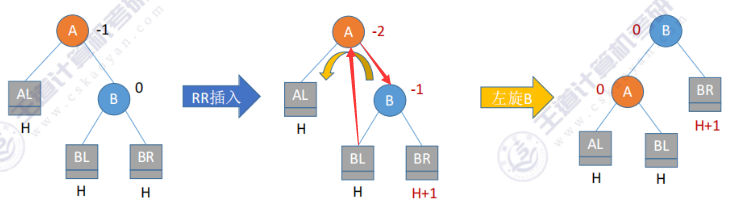
代码思路：我将之称之为找爸爸，依次从最小辈份的节点开始，首先是B的孩子找到现在的爸爸A，然后是A找到现在的爸爸B，最后是B找到现在的爸爸gf，即BL/BR→A→B→gf

代码思路

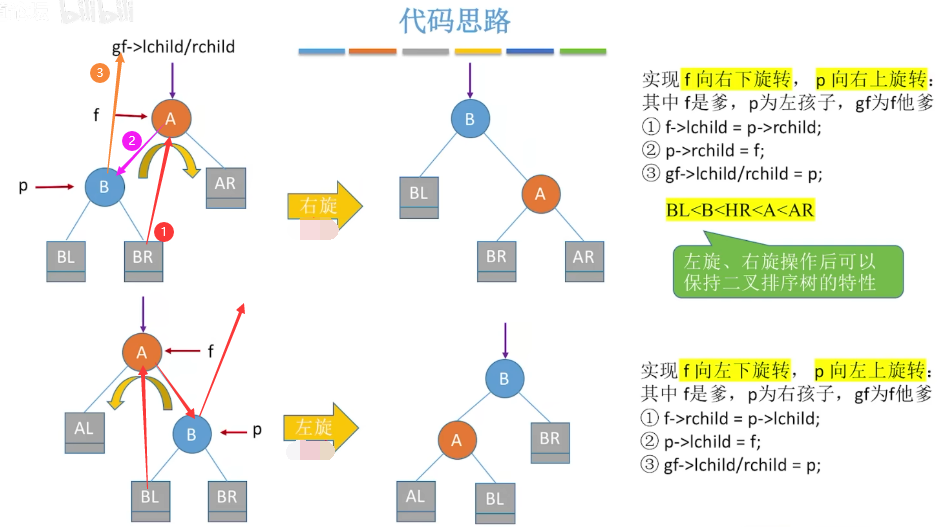
LR型：相当于先把C的左边部分拽下来，再把C的右边部分拽下来

左右双旋

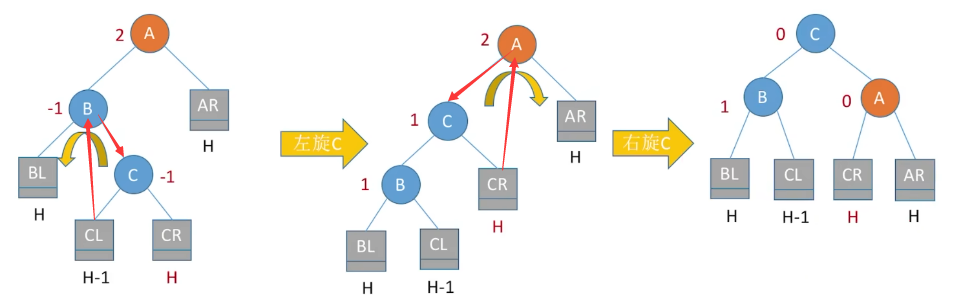
RL型

右左双旋

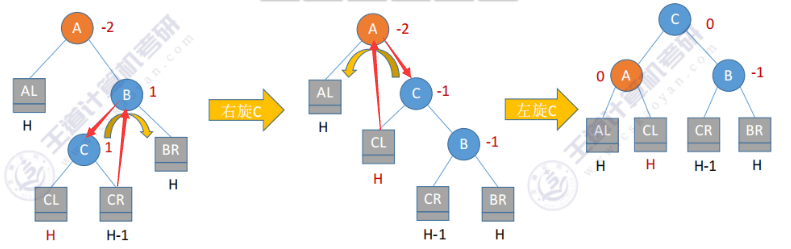
思路：

M形操作

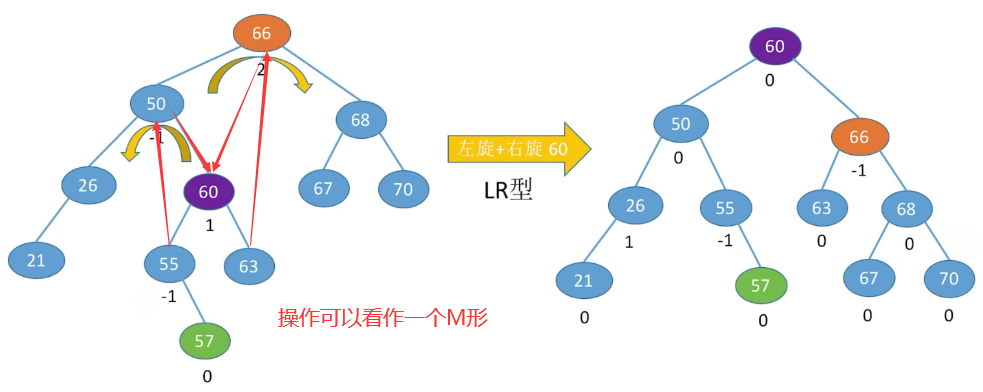
总结

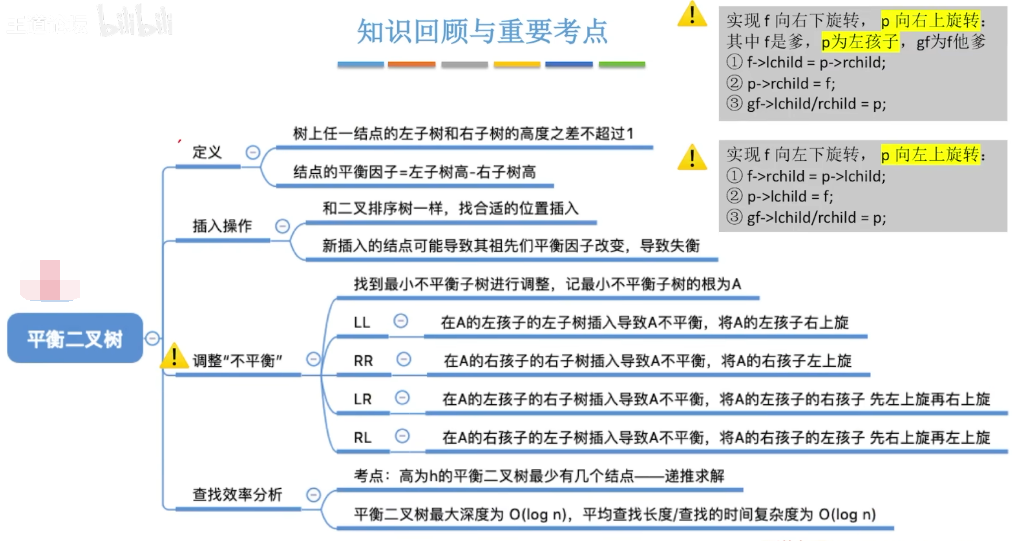
删除

和插入操作很类似，同样需要进行平衡性的检查。

Step：

用BST方法对节点X进行删除
若出现不平衡现象则从节点X向上进行回溯（向上找最小不平衡子树），找到第一个不平衡节点A，B为节点A最近的孩子节点，C是B最近的孩子节点（找“个头”最高的儿孙节点），然后以A为根，利用与插入相同的四种调整方法进行判断调整（LL、RR、LR、RL）
如果还是不平衡就继续向上，重复第2步
注：删除和插入对结点的调整方式大差不差，buttt插入仅针对最小不平衡子树A，而删除可能要一直“回溯”。

查找：AVL中查找操作与BST相同，因此查找时与给定值比较的关键字个数不超过树高，因此，含n个节点的AVL树的最大深度为，因此AVL的平均查找长度为

平衡二叉树的删除操作具体步骤：
①删除结点（方法同“二叉排序树”）
• 若删除的结点是叶子，直接删。
• 若删除的结点只有一个子树，用子树顶替删除位置
• 若删除的结点有两棵子树，用前驱（或后继）结点
顶替，并转换为对前驱（或后继）结点的删除。
②一路向北找到最小不平衡子树，找不到就完结撒花
③找最小不平衡子树下，“个头”最高的儿子、孙子
④根据孙子的位置，调整平衡（LL/RR/LR/RL）

• 孙子在LL：儿子右单旋
• 孙子在RR：儿子左单旋
• 孙子在LR：孙子先左旋，再右旋
• 孙子在RL：孙子先右旋，再左旋

⑤如果不平衡向上传导，继续②

不平衡子树恢复平衡后，高度变矮，可能使得上面的树出现不平衡现象

红黑树

为什么要发明红黑树？

平衡二叉树 AVL：插入/删除很容易破坏“平衡”特性，需要频繁调整树的形态。如：插入操作导致不平衡，则需要先计算平衡因子，找到最小不平衡子树（时间开销大），再进行 LL/RR/LR/RL 调整。适用于以查为主、很少插入/删除的场景

红黑树 RBT：插入/删除很多时候不会破坏“红黑”特性，无需频繁调整树的形态。即便需要调整，一般都可以在常数级时间内完成。适用于频繁插入、删除的场景，实用性更强

红黑树不是二叉平衡树，是BST（二叉排序树），与普通BST相比，有什么要求

①每个结点或是红色，或是黑色的
②根节点是黑色的
③叶结点（外部结点、NULL结点、失败结点）均是黑色的
④不存在两个相邻的红结点（即红结点的父节点和孩子结点均是黑色）
⑤对每个结点，从该节点到任一叶结点的简单路径上，所含黑结点的数目相同

总结为下面的口诀：

左根右（大小关系），根叶黑（颜色）
不红红(不能出现两个连续的红节点)，黑路同（黑节点数目）

struct RBnode{
    int key;	// 关键字的值
    RBnode* parent;
    RBnode* lChild;
    RBnode* rChild;
    int color;	//结点颜色，如:可用 0/1 表示 黑/红，也可使用枚举型enum表示颜色
};

黑高

结点的黑高 bh：从某结点出发（不含该结点）到达任一空叶结点的路径上黑结点总数

根节点黑高为h，则内部节点（关键字）至少有 2^h^-1 个
根节点黑高为h，内部结点数（关键字）至多有 2^2h^-1 个

内部结点数最少的情况——h层全黑结点的满树形态，因为全是黑色节点，只有满树形态才能保证黑路同
内部结点数最多的情况——h层黑结点，每一层黑结点下面都铺满一层红结点。共2h层的满树形态

性质

从根节点到叶节点的最长路径不大于最短路径的 2 倍（由④⑤得来，因为黑节点数目相同，所以相差最大的就是红结点穿插在黑节点之间）

任何一条查找失败路径上黑结点数量都相同，而路径上不能连续出现两个红结点，即红结点只能穿插在各个黑结点中间
有n个内部节点的红黑树的高度h ≤ 2𝑙𝑜𝑔2(𝑛 + 1)

若红黑树总高度=h，则根节点黑高 ≥ h/2，因此内部结点数 n ≥ 2h/2-1，由此推出 h ≤ 2𝑙𝑜𝑔2(𝑛 + 1)
红黑树的黑高（根节点到叶节点路径上黑色节点数量）至少为 h/2
红黑树查找操作时间复杂度 = O(log2n)

插入

插入节点使需要判断是否破环了红黑树性质，只用判断是否违反了不红红，因为插入红色节点满足左根右，根叶黑，黑路同。

先查找，确定插入位置（原理同二叉排序树），插入新结点

新结点是根——染为黑色
新结点非根——染为红色

查看插入新结点后是否满足不红红，若依然满足，则插入结束，若不满足，根据其叔叔（父节点的兄弟节点）的颜色进行相应调整

黑叔：旋转+染色（染色就是换成和之前不同的颜色）
- LL型：右单旋，父换爷+互换色（指给父和原爷节点染色）
- RR型：左单旋，父换爷+染色
- LR型：左、右双旋，儿换爷+染色（指给儿和原爷节点染色）
- RL型：右、左双旋，儿换爷+染色
红叔：染色+变新
- 叔父爷染色，爷变为新结点

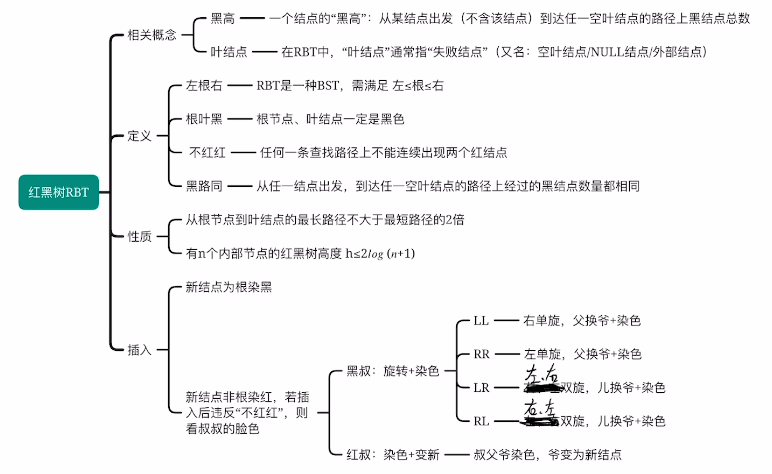
删除

重要考点：

红黑树删除操作的时间复杂度 = ==O(log2n)==
在红黑树中删除结点的处理方式和 ==二叉排序树的删除== 一样
按②删除结点后，可能破坏“红黑树特性”，此时需要调整结点==颜色、位置==，使其再次满足“红黑树特性”。

B树

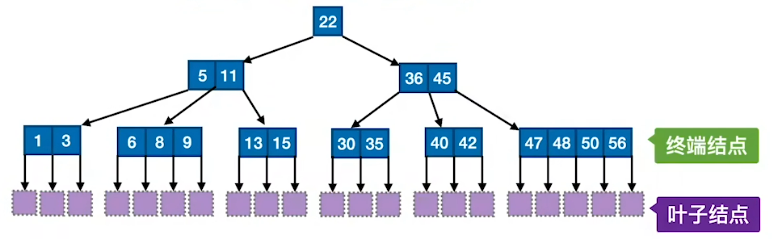
B树，又称多路平衡查找树，B树中所有结点的孩子个数的最大值称为B树的阶，通常用m表示。一棵m阶B树或为空树，或为满足如下特性的m叉树：

树中每个结点至多有m棵子树，即至多含有m-1个关键字。
若根结点不是终端结点，则至少有两棵子树。
除根结点外的所有非叶结点至少有 ⌈m/2⌉棵子树，即至少含有 ⌈m/2⌉-1 个关键字。（为了保证查找效率，每个结点的关键字不能太少）
所有的叶结点都出现在同一层次上，并且不带信息（可以视为外部结点或类似于折半查找判定树的查找失败结点，实际上这些结点不存在，指向这些结点的指针为空)。
所有非叶结点的结构如下：
｛n，P0，K1，P1，K2，…，Pn，Kn｝

其中， Ki 为结点的关键字，且依次递增：Pi 为指向子树根结点的指针，且指针Pi-1所指子树中所有结点的关键字均小于Ki，Pi所指子树中所有结点的关键字均大于Ki，n（ ⌈m/2⌉-1 ≤ n ≤ m-1 ）为结点中关键字的个数。

m阶B树的核心特性：

1）根节点的⼦树数∈[2, m]，关键字数∈[1, m-1]。其他结点的⼦树数∈[ , m]；关键字数∈[ -1, m-1]

2）对任⼀结点，其所有⼦树⾼度都相同

3）关键字的值：⼦树0<关键字1<⼦树1<关键字2<⼦树2<…. (类⽐⼆叉查找树左<中<右)

B树的高度：

B树的高度

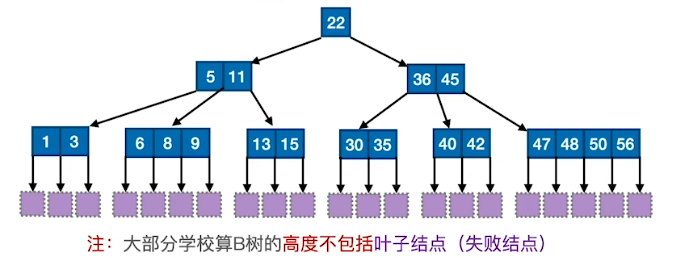
含 n 个关键字的 m叉B树，最小高度、最大高度是多少？

最大高度——让各层的分叉尽可能的少，即根节点只有2个分叉，其他结点只有[m/2]个分叉
各层结点至少有：第一层1、第二层2、第三层 2[m/2] …第h层2([m/2])-2
第h+1层共有叶子结点（失败结点） 2([m/27)^(h-1)
n个关键字的B树必有n+1个叶子结点，则 n+1≥2( ⌈m/ 2⌉^(h-1) ，即h ≤log~~⌈m/2⌉~~(n+1)/2+1

插入

删除

B+树

散列查找

loyeh

http://Lo-Y-eH.github.io/posts/c1a6/

本博客所有文章除特別声明外，均采用 CC BY 4.0 许可协议。转载请注明来源 loyeh !

查找

阅读全文

词缀助记

2024-07-15 笔记

词缀

阅读全文

并查集

2024-06-23 笔记

并查集

查找

查找

线性结构

顺序查找

折半查找

分块查找

树型结构

二叉排序树(BST)

查找

插入

递归实现

非递归实现

删除

平衡二叉树（AVL）

插入

删除

红黑树

黑高

性质

插入

删除

B树

插入

删除

B+树

散列查找

您的肯定是我前进的动力